Data Structures and Algorithms: Binary Search

The Binary Search Algorithm
 The binary search algorithm is a divide and conquer type algorithm, the idea behind the binary search is that the first comparison is done in the middle of the list if the item that we are searching for is it in the middle, the searching is complete, if the item we are searching is smaller then the item in the middle we are going to repeat the process on the left half of the list, or if the item we are searching is bigger then the item in the middle, we are going to search on the right side of the list. The initial size of searching is the entire list, but on each round, the size shrinks so the new size is half as big as the previous size. An important thing to remember about the binary search is that this type of search to work the list must be sorted in order. If the items in the list are not sorted, the most efficient search to be used is a linear search.
The binary search algorithm is a divide and conquer type algorithm, the idea behind the binary search is that the first comparison is done in the middle of the list if the item that we are searching for is it in the middle, the searching is complete, if the item we are searching is smaller then the item in the middle we are going to repeat the process on the left half of the list, or if the item we are searching is bigger then the item in the middle, we are going to search on the right side of the list. The initial size of searching is the entire list, but on each round, the size shrinks so the new size is half as big as the previous size. An important thing to remember about the binary search is that this type of search to work the list must be sorted in order. If the items in the list are not sorted, the most efficient search to be used is a linear search.
The divide-and-conquer paradigm is often used to find an optimal solution to a problem. The basic idea behind divide-and-conquer is to decompose a given problem into two or more similar, but simpler, subproblems, to solve them in turn, and to compose their solutions to solve the given problem.
Implementing Binary Search Algorithm
A binary search algorithm is not too complex for implementation, and it is very practical if the list is sorted (as we said before if the list is not sorted the binary search algorithm will not work!). Let's see an example of a binary search algorithm in Python.
def binarySearch(a, x):
"Binary search to find x in list a"
lower = -1
upper = len(a)
while upper > lower + 1:
mid = (lower + upper) // 2
if a[mid] == x:
return mid
if x < a[mid]:
upper = mid
else:
lower = mid
return None
Binary search imlementation in Python
At the start of our binary search algorithm example, we are defining a function named: binarySearch which accept two arguments(a and x) where a is the list and the x is the item we are searching for in the list. Inside the binarySearch function we have two variables lower and upper which will be the initial points where we start and stop with searching in the list. At any point in the binary search algorithm, lower will be one index less
then the index of the first item in the region and upper will be one more than the index of the last item in the region. The first step on each round of the binary search algorithm is to compute the location in the middle of the region. If the item we are searching for (x) is at that location the search terminates successfully. Otherwise, we need to find the middle of the region. It’s simply the index value that is halfway between lower and upper:
mid = (lower + upper) // 2
If the list item at this location is equal to x, the value we are searching for, we return mid as the final result. If the item is not at the midpoint we have to continue the search, and we will reduce the size of the region. To do that we simply have to move one of the boundaries so it is equal to the current midpoint.
Analysis of Binary Search Algorithm
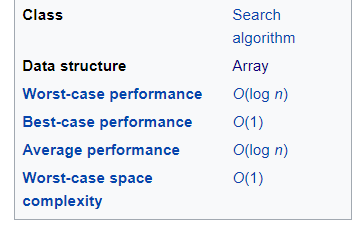
For a given list with n size of items, the best case is when the value is equal to the first item of the list O(1), in which case only one comparison is needed. If we know that the item is in the list, the worst case will be the O(log n) eg. the first or the last item because we have to do a maximum number of comparisons. In terms of average performances, no search algorithm that works only by comparing items can have better average performance than binary search which is O(log n).
If you want to learn more in-depth about algorithms and data structures, I highly recommend you to check this book: Introduction to Algorithms, 3rd Edition (The MIT Press)