Data Structures and Algorithms: Insertion Sort

The Insertion Sort Algorithm
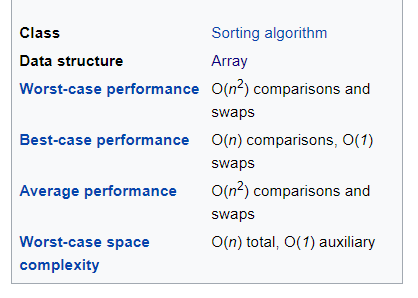 Insertion sort is a simple sorting algorithm that builds the final sorted array one item at a time. This algorithm is a simple technique that is easy to understand and implement. The steps done by this algorithm are an iterative solution of how a complex problem can be solved by repeatedly executing very simple steps. To understand how the insertion sort works, imagine that you have a couple of cards in one hand and you need to put them in order of their rank. One way to do it is to make sure cards on the left side in your have been sorted. Then pick up the third card (which is first not sorted) and place it on proper order among the first two cards. At any point in this process, we have two parts, the left part which is sorted and the right part which is not sorted. After each round of insertions, the sorted part grows longer, and the algorithm stops when the last card has been placed where it belongs and the entire hand is sorted.
Insertion sort is a simple sorting algorithm that builds the final sorted array one item at a time. This algorithm is a simple technique that is easy to understand and implement. The steps done by this algorithm are an iterative solution of how a complex problem can be solved by repeatedly executing very simple steps. To understand how the insertion sort works, imagine that you have a couple of cards in one hand and you need to put them in order of their rank. One way to do it is to make sure cards on the left side in your have been sorted. Then pick up the third card (which is first not sorted) and place it on proper order among the first two cards. At any point in this process, we have two parts, the left part which is sorted and the right part which is not sorted. After each round of insertions, the sorted part grows longer, and the algorithm stops when the last card has been placed where it belongs and the entire hand is sorted.
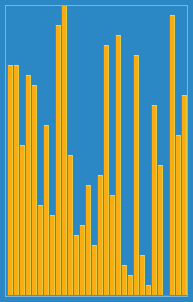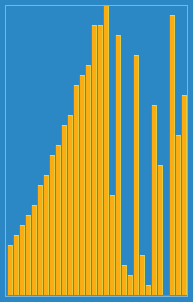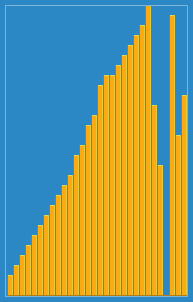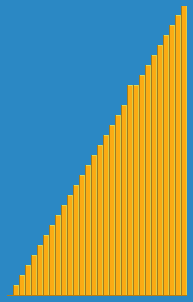
Insertion sort algorithm visual example
Implementing Insertion Sort Algorithm
Insertion sort algorithm is simple to implement, if we want to write an insertion sort algorithm we will need to use a for-loop inside the main function which we will be using it to iterate over all of the elements in the list and a while-loop inside the helper function which will be doing the most of the work. Let's see an example of an insertion sort algorithm in Python.
#insertion sort function
def insertionSort(a):
for i in range(1, len(a)):
moveLeft(a, i)
#helper function that moves a[j]
def moveLeft(a, j):
x = a.pop(j)
while j > 0 and a[j - 1] > x:
j -= 1
a.insert(j, x)
Insertion sort imlementation in Python
At the beginning of the example, we are defining a function insertionSort with one argument (a) which is the list. Inside the function, we have a for-loop that iterates through every element from the 1 (which is the second element, because the first is already sorted) to the end at the size of the list. Inside we have a helper function called moveLeft where we pass the reference to the list as the first argument a and the current index j. Removing the item at a specified location is straightforward, we simply need to call a method named pop defined in the list class, and it will remove the object at location j and saves it in x. On the next line, we have a while-loop that implements our leftward scan. Because j is the location where x was used to be, the first time the program executes the while-loop it will compare x to the item that was to its left. If the element on the left is larger it will need to go further to the left. The line with the j -= 1 in the while-loop subtracts one from j. On the last line, we simply insert the x at index j into the list a.
Analysis of Insertion Sort Algorithm
The best case input about the insertion sort algorithm is when the list is already sorted, which has a linear running time (i.e., O(n)). The worst-case input is when the list is sorted in reverse order, this gives us a quadratic running time (i.e., O(n2)). The average case is also quadratic, which puts insertion sort not very useful for sorting large lists. However, insertion sort is one of the fastest algorithms for sorting very small lists. For a given list with n size of items, the best case is when the value is equal to the first element of the list, in which case only one comparison is needed. The worst case is when the value is not in the list or occurs only once at the end of the list, in which case n comparisons are needed.
If you want to learn more in-depth about algorithms and data structures, I highly recommend you to check this book: Introduction to Algorithms, 3rd Edition (The MIT Press)
Tweet